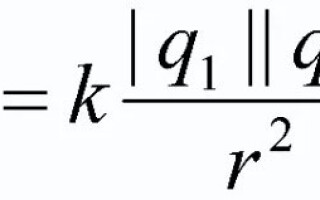ચાર્જ થયેલ સંસ્થાઓ વચ્ચે એક ક્રિયાપ્રતિક્રિયા બળ હોય છે જેના કારણે તેઓ એકબીજાને આકર્ષી શકે છે અથવા ભગાડી શકે છે. કુલોમ્બનો કાયદો આ બળનું વર્ણન કરે છે, શરીરના કદ અને આકારના આધારે તેની ક્રિયાની ડિગ્રી દર્શાવે છે. આ ભૌતિક કાયદાની આ લેખમાં ચર્ચા કરવામાં આવશે.
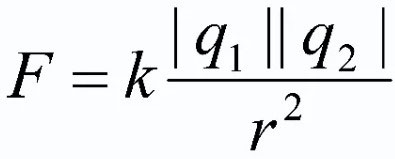
સામગ્રી
સ્થિર બિંદુ શુલ્ક
કુલોમ્બનો નિયમ સ્થિર સંસ્થાઓને લાગુ પડે છે જે અન્ય પદાર્થોથી તેમના અંતર કરતાં ઘણી ઓછી હોય છે. એક બિંદુ ઇલેક્ટ્રિક ચાર્જ આવા શરીર પર કેન્દ્રિત છે. શારીરિક સમસ્યાઓ હલ કરતી વખતે, માનવામાં આવેલા શરીરના પરિમાણોને અવગણવામાં આવે છે, કારણ કે તેઓ ખરેખર વાંધો નથી.
વ્યવહારમાં, બાકીના બિંદુ શુલ્ક નીચે પ્રમાણે દર્શાવવામાં આવ્યા છે:


આ કિસ્સામાં q1 અને q2 - આ છે હકારાત્મક ઇલેક્ટ્રીક ચાર્જિસ, અને કુલોમ્બ બળ તેમના પર કાર્ય કરે છે (આકૃતિમાં બતાવેલ નથી). બિંદુ લક્ષણોનું કદ કોઈ વાંધો નથી.
નૉૅધ! બાકીના ચાર્જ એકબીજાથી આપેલ અંતર પર સ્થિત છે, જે સમસ્યાઓમાં સામાન્ય રીતે અક્ષર r દ્વારા સૂચવવામાં આવે છે. આગળ લેખમાં, આ શુલ્ક વેક્યૂમમાં ધ્યાનમાં લેવામાં આવશે.
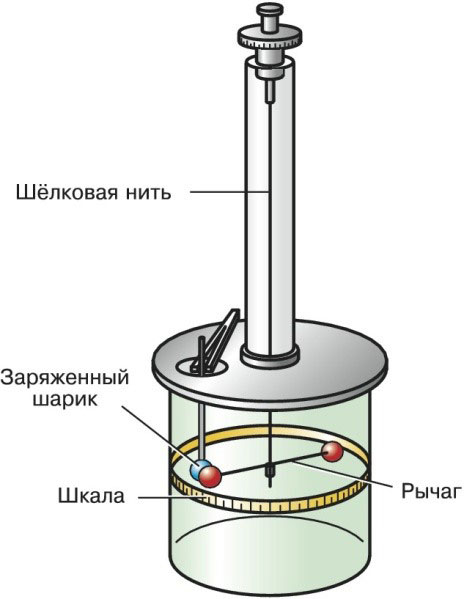
ચાર્લ્સ કુલોમ્બનું ટોર્સિયન બેલેન્સ
1777માં કુલોમ્બ દ્વારા વિકસાવવામાં આવેલ આ ઉપકરણ, પાછળથી તેમના નામ પર રાખવામાં આવેલ બળની અવલંબનને કાઢવામાં મદદ કરી. તેની મદદથી, બિંદુ શુલ્કની ક્રિયાપ્રતિક્રિયા, તેમજ ચુંબકીય ધ્રુવોનો અભ્યાસ કરવામાં આવે છે.
ટોર્સિયન બેલેન્સમાં એક નાનો રેશમનો દોરો હોય છે જે વર્ટિકલ પ્લેનમાં સ્થિત હોય છે જેમાંથી સંતુલિત લિવર અટકે છે. પોઈન્ટ ચાર્જ લીવરના છેડે સ્થિત છે.
બાહ્ય દળોની ક્રિયા હેઠળ, લિવર આડા ખસેડવાનું શરૂ કરે છે. જ્યાં સુધી તે થ્રેડના સ્થિતિસ્થાપક બળ દ્વારા સંતુલિત ન થાય ત્યાં સુધી લીવર પ્લેનમાં આગળ વધશે.
ચળવળની પ્રક્રિયામાં, લીવર ચોક્કસ કોણ દ્વારા ઊભી અક્ષથી વિચલિત થાય છે. તેને d તરીકે લેવામાં આવે છે અને તેને પરિભ્રમણનો કોણ કહેવામાં આવે છે. આ પરિમાણના મૂલ્યને જાણીને, ઉદ્ભવતા દળોના ટોર્કને શોધવાનું શક્ય છે.
ચાર્લ્સ કુલોમ્બનું ટોર્સિયન બેલેન્સ આના જેવું દેખાય છે:
પ્રમાણસરતા પરિબળ k અને વિદ્યુત સ્થિરાંક 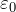
કુલોમ્બના કાયદાના સૂત્રમાં પરિમાણો k છે - પ્રમાણસરતાનો ગુણાંક અથવા ![]() વિદ્યુત સ્થિરાંક છે. વિદ્યુત સ્થિર
વિદ્યુત સ્થિરાંક છે. વિદ્યુત સ્થિર ![]() ઘણા સંદર્ભ પુસ્તકો, પાઠ્યપુસ્તકો, ઈન્ટરનેટમાં પ્રસ્તુત છે અને તેને ગણવાની જરૂર નથી! વેક્યુમ પ્રમાણસરતા પરિબળ પર આધારિત છે
ઘણા સંદર્ભ પુસ્તકો, પાઠ્યપુસ્તકો, ઈન્ટરનેટમાં પ્રસ્તુત છે અને તેને ગણવાની જરૂર નથી! વેક્યુમ પ્રમાણસરતા પરિબળ પર આધારિત છે ![]() જાણીતા સૂત્ર દ્વારા શોધી શકાય છે:
જાણીતા સૂત્ર દ્વારા શોધી શકાય છે:
![]()
અહીં ![]() વિદ્યુત સ્થિરાંક છે,
વિદ્યુત સ્થિરાંક છે,
![]() - પી,
- પી,
![]() શૂન્યાવકાશમાં પ્રમાણસરતાનો ગુણાંક છે.
શૂન્યાવકાશમાં પ્રમાણસરતાનો ગુણાંક છે.
વધારાની માહિતી! ઉપર પ્રસ્તુત પરિમાણોને જાણ્યા વિના, તે બે બિંદુ ઇલેક્ટ્રિક ચાર્જ વચ્ચે ક્રિયાપ્રતિક્રિયાના બળને શોધવાનું કામ કરશે નહીં.
કુલોમ્બના કાયદાની રચના અને સૂત્ર
ઉપરોક્ત સારાંશ આપવા માટે, ઇલેક્ટ્રોસ્ટેટિક્સના મુખ્ય કાયદાની સત્તાવાર રચના આપવી જરૂરી છે. તે ફોર્મ લે છે:
શૂન્યાવકાશમાં બાકી રહેલા બે બિંદુ ચાર્જની ક્રિયાપ્રતિક્રિયાનું બળ આ ચાર્જના ઉત્પાદનના સીધા પ્રમાણસર છે અને તેમની વચ્ચેના અંતરના વર્ગના વિપરિત પ્રમાણસર છે. તદુપરાંત, શુલ્કનું ઉત્પાદન મોડ્યુલો લેવું આવશ્યક છે!
![]()
આ સૂત્રમાં q1 અને q2 પોઈન્ટ ચાર્જિસ છે, જે સંસ્થાઓ ગણવામાં આવે છે; આર2 - ચોરસમાં લેવામાં આવેલા આ સંસ્થાઓ વચ્ચેના પ્લેન પરનું અંતર; k એ પ્રમાણનો ગુણાંક છે (![]() વેક્યુમ માટે).
વેક્યુમ માટે).
કુલોમ્બ બળની દિશા અને સૂત્રનું વેક્ટર સ્વરૂપ
સૂત્રની સંપૂર્ણ સમજણ માટે, કુલોમ્બના કાયદાની કલ્પના કરી શકાય છે:
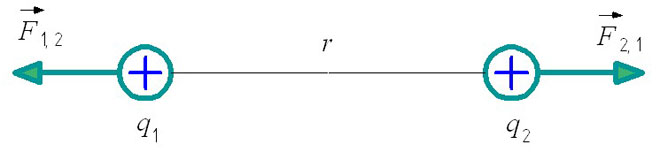
એફ1,2 - બીજાના સંદર્ભમાં પ્રથમ ચાર્જની ક્રિયાપ્રતિક્રિયાનું બળ.
એફ2,1 - પ્રથમના સંબંધમાં બીજા ચાર્જની ક્રિયાપ્રતિક્રિયાનું બળ.
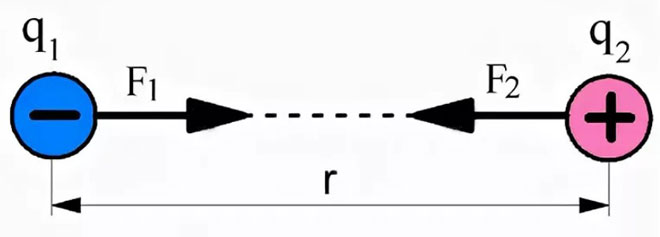
ઉપરાંત, ઇલેક્ટ્રોસ્ટેટિક્સની સમસ્યાઓ હલ કરતી વખતે, એક મહત્વપૂર્ણ નિયમ ધ્યાનમાં લેવો જરૂરી છે: સમાન નામના ઇલેક્ટ્રિક ચાર્જને ભગાડે છે, અને વિપરીત ચાર્જ આકર્ષે છે. આકૃતિમાં ક્રિયાપ્રતિક્રિયા દળોનું સ્થાન આના પર નિર્ભર છે.
જો વિરોધી શુલ્ક ધ્યાનમાં લેવામાં આવે, તો તેમની ક્રિયાપ્રતિક્રિયાના દળો એકબીજા તરફ નિર્દેશિત કરવામાં આવશે, તેમના આકર્ષણનું નિરૂપણ કરશે.
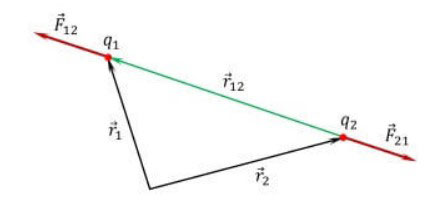
વેક્ટર સ્વરૂપમાં ઇલેક્ટ્રોસ્ટેટિક્સના મૂળભૂત કાયદાના સૂત્રને નીચે પ્રમાણે રજૂ કરી શકાય છે:
![]()
![]() ચાર્જ q2 ની બાજુથી, બિંદુ ચાર્જ q1 પર કાર્ય કરતું બળ છે,
ચાર્જ q2 ની બાજુથી, બિંદુ ચાર્જ q1 પર કાર્ય કરતું બળ છે,
![]() ચાર્જ q2 ને ચાર્જ q1 સાથે જોડતો ત્રિજ્યા વેક્ટર છે,
ચાર્જ q2 ને ચાર્જ q1 સાથે જોડતો ત્રિજ્યા વેક્ટર છે,
![]()
મહત્વપૂર્ણ! સૂત્રને વેક્ટર સ્વરૂપમાં લખ્યા પછી, ચિહ્નોને યોગ્ય રીતે મૂકવા માટે બે બિંદુ ઇલેક્ટ્રિક ચાર્જની ક્રિયાપ્રતિક્રિયા કરતી દળોને ધરી પર પ્રક્ષેપિત કરવાની જરૂર પડશે. આ ક્રિયા એક ઔપચારિકતા છે અને ઘણી વખત કોઈપણ નોંધ વિના માનસિક રીતે કરવામાં આવે છે.
જ્યાં કુલોમ્બનો કાયદો વ્યવહારમાં લાગુ થાય છે
ઈલેક્ટ્રોસ્ટેટિક્સનો મૂળભૂત કાયદો ચાર્લ્સ કુલોમ્બની સૌથી મહત્વપૂર્ણ શોધ છે, જેણે ઘણા ક્ષેત્રોમાં તેનો ઉપયોગ શોધી કાઢ્યો છે.
વિવિધ ઉપકરણો, ઉપકરણો, ઉપકરણોની શોધની પ્રક્રિયામાં પ્રખ્યાત ભૌતિકશાસ્ત્રીના કાર્યોનો ઉપયોગ કરવામાં આવ્યો હતો. ઉદાહરણ તરીકે, વીજળીની લાકડી.
વીજળીના સળિયાની મદદથી, રહેણાંક ઇમારતો અને ઇમારતોને વાવાઝોડા દરમિયાન વીજળીથી સુરક્ષિત કરવામાં આવે છે. આમ, ઇલેક્ટ્રિકલ સાધનોના રક્ષણની ડિગ્રીમાં વધારો થાય છે.
વીજળીની લાકડી નીચેના સિદ્ધાંત અનુસાર કાર્ય કરે છે: વાવાઝોડા દરમિયાન, મજબૂત ઇન્ડક્શન ચાર્જ ધીમે ધીમે જમીન પર એકઠા થવાનું શરૂ થાય છે, જે ઉપર આવે છે અને વાદળો તરફ આકર્ષાય છે. આ કિસ્સામાં, જમીન પર એક જગ્યાએ વિશાળ ઇલેક્ટ્રિક ક્ષેત્ર રચાય છે. વીજળીના સળિયાની નજીક, ઇલેક્ટ્રિક ક્ષેત્ર વધુ મજબૂત બને છે, જેના કારણે ઉપકરણની ટોચ પરથી કોરોના ઇલેક્ટ્રિક ચાર્જ પ્રગટ થાય છે.
આગળ, જમીન પર રચાયેલ ચાર્જ વિરોધી ચિહ્ન સાથે વાદળના ચાર્જ તરફ આકર્ષિત થવાનું શરૂ કરે છે, કારણ કે તે ચાર્લ્સ કુલોમ્બના નિયમ મુજબ હોવું જોઈએ. તે પછી, હવા આયનીકરણની પ્રક્રિયામાંથી પસાર થાય છે, અને વીજળીના સળિયાના અંતની નજીક ઇલેક્ટ્રિક ક્ષેત્રની શક્તિ ઓછી થઈ જાય છે. આમ, મકાનમાં વીજળી પડવાનું જોખમ ન્યૂનતમ છે.
નૉૅધ! જે બિલ્ડિંગ પર લાઈટનિંગ સળિયો લગાવવામાં આવ્યો છે તે જો અથડાશે, તો આગ લાગશે નહીં, અને બધી ઊર્જા જમીનમાં જશે.
કુલોમ્બના કાયદાના આધારે, "પાર્ટિકલ એક્સિલરેટર" નામનું ઉપકરણ વિકસાવવામાં આવ્યું હતું, જે આજે ખૂબ માંગમાં છે.
આ ઉપકરણમાં, એક મજબૂત ઇલેક્ટ્રિક ક્ષેત્ર બનાવવામાં આવે છે, જે તેમાં પડતા કણોની ઊર્જાને વધારે છે.
કુલોમ્બના કાયદામાં દળોની દિશા
ઉપર સૂચવ્યા મુજબ, બે બિંદુ ઇલેક્ટ્રિક ચાર્જની ક્રિયાપ્રતિક્રિયા દળોની દિશા તેમની ધ્રુવીયતા પર આધારિત છે. તે. સમાન નામના શુલ્ક ભગાડશે, અને વિપરીત શુલ્કના શુલ્ક આકર્ષિત કરશે.
કુલોમ્બ દળોને ત્રિજ્યા વેક્ટર પણ કહી શકાય, કારણ કે તેઓ તેમની વચ્ચે દોરેલી રેખા સાથે નિર્દેશિત થાય છે.
કેટલીક શારીરિક સમસ્યાઓમાં, જટિલ આકારના શરીર આપવામાં આવે છે, જે બિંદુ ઇલેક્ટ્રિક ચાર્જ માટે લઈ શકાતા નથી, એટલે કે. તેના કદને અવગણો. આ સ્થિતિમાં, વિચારણા હેઠળના શરીરને કેટલાક નાના ભાગોમાં વિભાજિત કરવું આવશ્યક છે અને કુલોમ્બના કાયદાનો ઉપયોગ કરીને દરેક ભાગની અલગથી ગણતરી કરવી આવશ્યક છે.
વિભાજન દ્વારા મેળવેલા બળ વેક્ટરનો સારાંશ બીજગણિત અને ભૂમિતિના નિયમો અનુસાર કરવામાં આવે છે. પરિણામ પરિણામી બળ છે, જે આ સમસ્યાનો જવાબ હશે. ઉકેલવાની આ પદ્ધતિને ઘણીવાર ત્રિકોણ પદ્ધતિ કહેવામાં આવે છે.
કાયદાની શોધનો ઇતિહાસ
ઉપરોક્ત માનવામાં આવેલા કાયદા દ્વારા બે બિંદુ શુલ્કની ક્રિયાપ્રતિક્રિયાઓ પ્રથમ વખત 1785 માં ચાર્લ્સ કુલોમ્બ દ્વારા સાબિત કરવામાં આવી હતી. ભૌતિકશાસ્ત્રીએ ટોર્સિયન બેલેન્સનો ઉપયોગ કરીને ઘડેલા કાયદાની સત્યતાને સાબિત કરવામાં વ્યવસ્થાપિત કર્યું, જેનું સંચાલન સિદ્ધાંત પણ લેખમાં રજૂ કરવામાં આવ્યું હતું.
કુલોમ્બે એ પણ સાબિત કર્યું કે ગોળાકાર કેપેસિટરની અંદર કોઈ ઇલેક્ટ્રિક ચાર્જ નથી. તેથી તે નિવેદનમાં આવ્યો કે ઇલેક્ટ્રોસ્ટેટિક દળોની તીવ્રતા વિચારણા હેઠળના શરીર વચ્ચેના અંતરને બદલીને બદલી શકાય છે.
આમ, કુલોમ્બનો કાયદો હજુ પણ ઇલેક્ટ્રોસ્ટેટિક્સનો સૌથી મહત્વપૂર્ણ કાયદો છે, જેના આધારે ઘણી મહાન શોધો કરવામાં આવી છે. આ લેખના માળખામાં, કાયદાની સત્તાવાર શબ્દરચના રજૂ કરવામાં આવી હતી, તેમજ તેના ઘટક ભાગોનું વિગતવાર વર્ણન કરવામાં આવ્યું હતું.
સમાન લેખો: